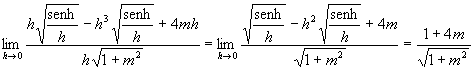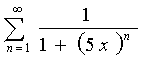
SOLUZIONE DEI QUESITI PROPOSTI
ALLA PROVA SCRITTA DEL 21-06-2000
1) Studiare la convergenza puntuale ed uniforme della serie:
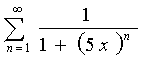
Per studiare la convergenza puntuale della serie di funzioni si fa il limite:
.
Dunque la serie converge puntualmente alla funzione 
.
Condizione necessaria perché la serie converga uniformemente è che:
essendo la serie limitata il sup coincide con il massimo della funzione:
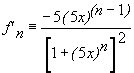
e si annulla per x=0, in questo punto 
; quindi la serie non converge uniformemente.
2) Stabilire se in (0,0) risulta continua,derivabile e differenziabile la funzione f definita da:
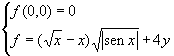
CONTINUITA’ IN (0,0):
DERIVABILITA IN (0,0):
Affinché la funzione sia derivabile i seguenti limiti devono esistere ed essere finiti:
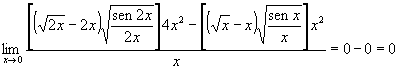
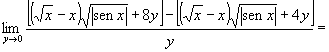
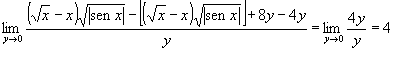
I due limiti esistono e sono finiti dunque f è derivabile in (0,0).
DIFFERENZIABILITA IN (0,0):
Affinché la funzione sia differenziabile si deve verificare che:
.
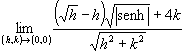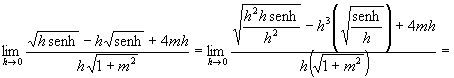
