PROGRAMMA DEL CORSO DI
ANALISI MATEMATICA II
(corso di laurea in Fisica)
Prof.ssa P.Di Gironimo
Integrale di Riemann per funzioni di una variabile
- Il metodo di esaustione: definizione; calcolo dell'area di un settore di parabola.
- Integrale di Riemann
: definizione e proprietà. C.N.S. per l’integrabilità secondo Riemann. Integrabilità delle funzioni continue(c.d.) e delle funzioni monotone. Teorema della media integrale (c.d).Proprietà degli integrali. Integrale definito. Il teorema fondamentale del calcolo integrale. Metodo di integrazione definita per parti. Metodo di integrazione definita per sostituzione.
- Integrali impropi
: Assoluta integrabilità. Criteri di esistenza degli integrali impropi.
Serie numeriche
Serie numeriche: Definizione. Criterio di Cauchy . Condizione necessaria per la convergenza. La serie geometrica.
Criteri di convergenza per le serie a termini positivi: La serie armonica e serie armonica generalizzata. Serie a termini non negativi. La serie di Riemann. Teorema di confronto ed applicazioni. Criterio della radice e del rapporto.
Serie alternate: convergenza . Serie armonica alternata.Criterio di Leibniz.
Serie assolutamente convergenti: definizione, convergenza delle serie assolutamente convergenti
Successioni e serie di funzioni
Successioni di funzioni: convergenza puntuale ed uniforme. Teorema del Dini.
Serie di funzioni: convergenza puntuale ed uniforme. Serie totalmente convergente. Integrazione e derivazione termine a termine.
Serie di potenze: Intervallo e raggio di convergenza. Calcolo del raggio di convergenza. Teorema di Abel. Analiticità delle serie di potenze nell’intervallo di convergenza.
Serie di Taylor: Sviluppabilità in serie di Taylor.
Serie di Fourier
Funzioni periodiche: definizione e proprietà.
Serie di Fourier: calcolo dei coefficienti di Fourier relativi ad una funzione f(x); funzioni pari e funzioni dispari; disuguaglianza di Bessel.
Sviluppabilità in serie di Fourier: sviluppabilità di una funzione periodica in serie di Fourier; risultati di convergenza della serie di Fourier.
integrazione di una serie di Fourier.
Spazi metrici e spazi di Banach
Spazi metrici: Esempi di spazi metrici ,metrica euclidea su R, metrica del sup nello spazio C(A). Disuguaglianza di Cauchy-Schwarz. Successioni convergenti e funzioni continue in uno spazio metrico. Teorema di separazione.
Spazi vettoriali: Applicazioni lineari. Lo spazio vettoriale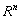 
e il suo duale. Spazi vettoriali normati
Spazi metrici completi: Spazi di Banach:
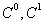. Funzioni Lipschitziane. Il teorema delle contrazioni. Insiemi compatti; funzioni continue sui compatti, Teorema di Cantor. Aperti connessi di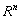
.
Funzioni di più variabili
Richiami di topologia in .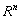
Funzioni di più variabili: Limiti. Continuità. Derivate parziali. Derivate successive. Matrice hessiana. Il teorema di Schwarz.
Gradiente e differenziabilità: Rappresentazione del differenziale mediante il gradiente. Base duale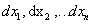 
ed espressione del differenziale. Differenziabilità e continuità. Teorema del differenziale totale. Piano tangente.
Teorema di derivazione delle funzioni composte. Differenziabilità delle funzioni
composte
- Derivata direzionale
: definizione , derivata direzionale di una funzione differenziabile. Funzioni con gradiente nullo in un connesso. Funzioni definite mediante integrali.
- Formula di Taylor:
Formula di Taylor e differenziali di ordine superiore.
- Forme quadratiche
. Matrici quadrate definite, semi definite e in definite. Caratterizzazione delle matrici definite. Caratterizzazione delle matrici 2x2.
- Massimi e minimi relativi
. Condizione necessaria del primo ordine. Matrice hessiana. Condizione necessaria del secondo ordine. Condizione sufficiente nel caso di n variabili. Determinante hessiano. Condizione sufficiente nel caso di 2 variabili.
- Funzioni a valori vettoriali
: differenze tra le funzioni vettoriali e quelle scalari.
Definizione di campo vettoriale. C.N.eS. affinchè una funzione vettoriale sia
convergente. Definizione di matrice jacobiana. Teorema di differenziabilità di una
funzione vettoriale.Teorema di rappresentazione del gradiente e del differenziale
della funzione composta vettoriale.Teorema sullo jacobiano delle funzioni
composte. Formula di rappresentazione dello jacobiano dell’inversa di una
applicazione vettoriale.
Equazioni differenziali ordinarie
Equazioni differenziali: Esempi di equazioni differenziali lineari e non lineari, problema di Cauchy. Definizione di soluzione locale e di soluzione globale.
Equazioni differenziali di tipo normale di ordine n.
- Teorema di esistenza ed unicità locale per il problema di Cauchy
. Equazioni differenziali del primo ordine in forma normale:y’=f(x,y). Ipotesi di Lipschitz: condizione sufficiente. Formulazione integrale del problema di Cauchy . Teorema di esistenza ed unicità locale per il problema di Cauchy. Teorema di regolarità .
Teorema di Peano. Estensione del teorema di esistenza ed unicità locale per
sistemi di equazioni differenziali di ordine comunque elevato.
- Prolungamento delle soluzioni:
definizione e proprietà. Esistenza del prolungamento massimale.
- Teorema di esistenza ed unicità globale
: Teorema di esistenza ed unicità globale. Teorema di prolungamento.
Equazioni differenziali lineari di ordine n. Teorema di esistenza ed unicità.
Teorema sul Wronsiano.
Curve ed integrali curvilinei
: Definizione di curva; curva semplice e chiusa; curva regolare; curve equivalenti e curve orientate.Versore tangente. Lunghezza di una curva. Ascissa curvilinea. Integrale di una funzione su una curva ed invarianza per curve equivalenti.
Forme differenziali lineari
Forme differenziali: Integrale curvilineo di una forma differenziali: invarianza dell’integrale su curve equivalenti. Forme differenziali esatte. Indipendenza dal cammino di una forma differenziale esatta. Teorema di caratterizzazione delle forme esatte. Forme chiuse. Forme differenziali in un rettangolo di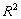 
e in un aperto semplicemente connesso di 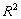. Forme differenziali in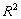
a coefficienti omogenei. Criterio di esattezza negli aperti stellati.
Integrali multipli
Integrali multipli su domini normali. Additività della misura. Formule di riduzione per gli integrali doppi. Primo teorema di Guldino. Formule di Gauss-Green; teorema della divergenza; formule di Stokes. Teorema di cambiamento di variabili negli integrali doppi. Integrali tripli.
Misura di Peano-Jordan e misura di Lebesgue
Misura secondo Peano-Jordan: Misura degli intervalli e dei plurintervalli superiormente semiaperti; finita additività della misura; misura interna ed esterna di un insieme limitato; insieme misurabile secondo Peano-Jordan.
Misura di Lebesgue: misura degli intervalli, dei plurintervalli, degli aperti e dei compatti. Proprietà di subadditività e superadditività finita su aperti e compatti. Misura interna e misura esterna di un insieme limitato. Confronto con la misura di Peano-Jordan.
Proprietà della misura: Subadditività della misura esterna e superadditività della misura interna. Additività finita sugli insiemi misurabili. Chiusura della famiglia degli insiemi misurabili rispetto a complemento intersezione ed unione finite. . Additività numerabile sugli insiemi misurabili. Insiemi misurabili non limitati; teorema sulle successioni monotone di insiemi misurabili.
Integrale di Lebesgue
Funzioni misurabili: definizione e proprietà,misurabilità della somma, del prodotto, del sup ed dell'inf. Funzioni semplici.
Integrale di Lebesgue di una funzione misurabile non negativa.
Toeremi di passaggio al limite sotto il segno di integrale: Teorema di Beppo Levi. Lemma di Fatou. Confronto tra l'integrale di Riemann e l'integrale di Lebesgue. Funzioni sommabili. Teorema di Lebesgue sulla convergenza dominata.
Funzioni integrabili. Teorema del sottografico. Teorema sulle sezioni di insiemi misurabili. Teorema sulla caratterizzazione delle funzioni misurabili. Teorema di Fubini.
Superfici ed integrali di superficie
Superfici: definizioni e proprietà Superfici regolari. Piano tangente e versore normale. Superfici equivalenti. Orientamento di una superficie. Area di una superficie regolare. Integrali di superficie. La formula di Stokes.
Funzioni implicite
Funzioni implicite: Teorema del Dini. Teorema sulla derivazione delle funzioni implicite. Teorema del Dini per funzioni a valori vettoriali. Invertibilità locale e globale. Massimi e minimi vincolati. Moltiplicatori di Lagrange.
TESTI CONSIGLIATI
F.Cafiero, Lezione di Analisi Matematica, parte seconda, Liguori.
N.Fusco-P.Marcellini-C.Sbordone, Analisi Matematica II, Liguori.
E.Giusti, Analisi Matematica II, Boringhieri.
M.Troisi, Analisi Matematica I, Liguori.