GRUPPO L

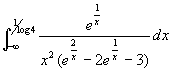
L'integrale è improprio, la funzione integranda è limitata negli estremi di integrazione. Quindi valutando la convergenza dell'integrale consideriamo:

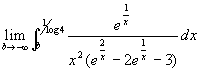
Effettuo la seguente sostituzione: per cui scrivo:

da cui

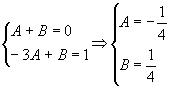
A questo punto calcolo il seguente integrale:

.

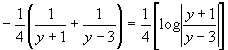Tenendo conto della sostituzione effettuata scrivo:

.

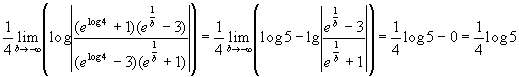Effettuo la seguente sostituzione: . Sapendo che: 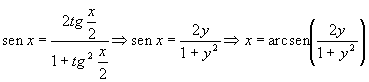, da cui

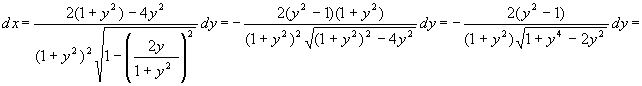
calcolo il seguente integrale:

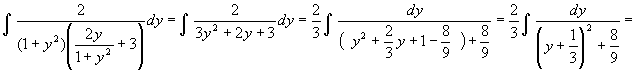
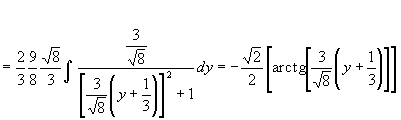
Tenendo conto della sostituzione effettuata, scrivo:

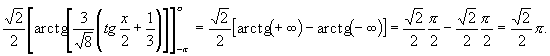
Dal momento che la serie numerica potrebbe essere convergente. Per verificarlo, uso il criterio del rapporto:

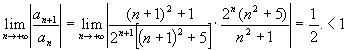
Siccome questo limite esiste ed è minore di 1, la serie è convergente.