Torna indietro

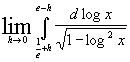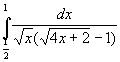
Gruppo G

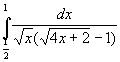
razionalizzando il denominatore si ottiene:

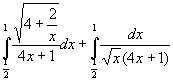risolviamo il primo integrale:

posto =tsostituendo nell’integrale si ottiene:

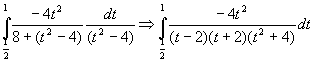decomponendo per fratti semplici si ottiene

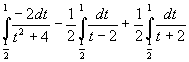= sostituendo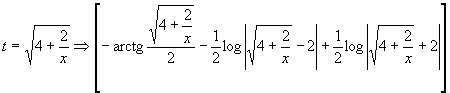

Calcoliamo il secondo integrale

sostituendo sostituendo nell’integrale si ha

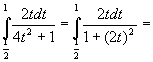
La soluzione finale è: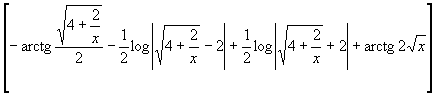valutando la funzione negli estremi di integrazione si ottiene:

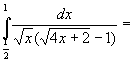
Applicando il criterio della radice si ha:

==

calcoliamo il limite dell’esponente:

essendo questa una forma indeterminata applichiamo il teorema di De L’Hopital:

=-log5 avendo applicato il principio degli infiniti

Dunque:

=

La serie converge.

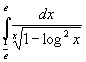
la funzione diverge negli estremi di integrazione

Essendo si ha:

==p