Gruppo F
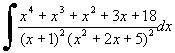
La funzione integranda è razionale fratta propria (grado del denominatore > del grado del
numeratore).
Il denominatore di tale funzione è con radici multiple ed anche complesse,
quindi scomponiamo tale frazione in somma di frazioni elementari del tipo:
(1)
Effettuiamo il m.c.m. e, per semplicità di scrittura, riportiamo solo il numeratore:
effettuando i vari calcoli otteniamo:
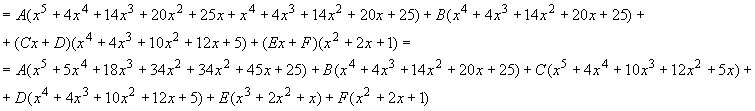
Applicando il principio di identità dei polinomi alla (1), otteniamo facilmente il seguente sistema:
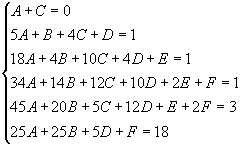
(2)
Risolvendo il sistema (2) con il metodo della sostituzione, otteniamo:
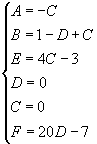
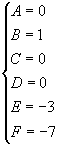
L'integrale di partenza può, quindi, essere decomposto tramite gli integrali (a )e(b )in:
Risolviamo separatamente (a ) e (b ):
Scriviamo (
) in modo da ottenere al denominatore una somma di quadrati:
Poniamo: 
Sostituendo in (
),otteniamo:
Abbiamo ottenuto () come combinazione lineare di due integrali più semplici, che denotiamo col simbolo (
) e (
):
Risolviamo separatamente () e (
):
Per quanto riguarda la risoluzione di (
), risolviamo per sostituzione;
poniamo: 
:
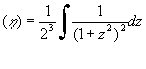
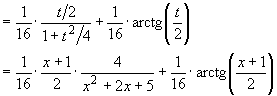
La soluzione del nostro integrale di partenza è, quindi:
ossia
Risolviamo per sostituzione,
ponendo: 
(3)
Risolviamo tale integrale utilizzando il metodo di integrazione per parti:
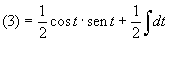
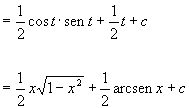
Si tratta di una serie di potenze di punto iniziale 
e di termine generale 
Calcoliamo il raggio di convergenza applicando il criterio del confronto:
Il raggio di convergenza , che denoto con r, è, quindi 3. Pertanto l'intervallo di convergenza puntuale è:
Per stabilire l'esistenza o meno di un intervallo di convergenza uniforme, studiamo la serie agli estremi. Otteniamo:
(*)
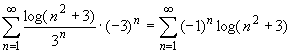
la serie diverge; non è soddisfatta, infatti, la condizione necessaria per la convergenza (il termine n-mo non è infinitesimo).
(**)
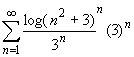
Anche in questo caso la serie diverge.