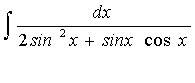
1)
Calcolare il seguente integrale:
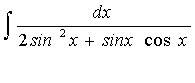
Dividendo numeratore e denominatore per cos2x,
si ha:
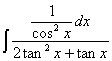
Posto 
=
, si ha :
=
Sostituendo:
=
=
=*
con 
e 
costanti da determinare col
principio d’identità dei polinomi.
=
.
Allora: 
=
=
=
í
í
=
=
Perciò:
*=
=
=
=
2) Studiare la convergenza puntuale e
uniforme della serie:
=
=
=
la serie
converge puntualmente
.
Per 
=
, 
=
=
, che è il termine generale di una
serie a termini di segno alternato.
Poiché il termine generale della serie non
è infinitesimo, tale serie non converge.
Per 
=
, 
=
, che è il termine generale di una
serie divergente, poiché 
=
L’intervallo di convergenza uniforme è
quindi 
.