La soluzione sarà del tipo
.
Risolviamo l’equazione omogenea associata:
Scriviamo il polinomio caratteristico:
.
Osserviamo che 
e 
non sono radici del polinomio 
;
imponiamo che 
sia soluzione
dell’equazione:
Sostituiamo nell’equazione di partenza:
Per il principio d’identità dei polinomi risulta:
2) Stabilire se in 
risulta continua, derivabile e differenziabile la funzione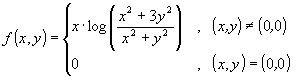 
Osserviamo che 
sempre 
continua 
Verifichiamo se 
:
Facciamo tendere 
ad 
lungo una retta del
fascio di centro 
e di equazione 
:
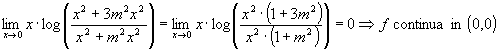
Ricordiamo che 
è differenziabile se:
.
Calcoliamo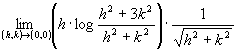 
;
ponendo 
, si ha:
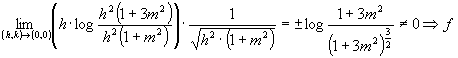non
differenziabile, poiché il limite non esiste.
Vediamo se 
ammette derivata in ogni direzione:
sia 
un vettore direzionale 
;
affinché 
ammetta derivata nella direzione 
,
deve esistere finito 
.
Si ha: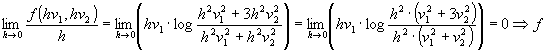
è derivabile.
;
