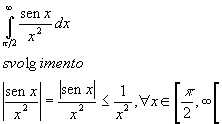
GRUPPO D
Studiare la convergenza dell'integrale
:
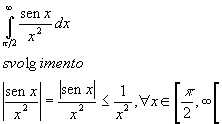
Essendo la funzione
integrabile impropriamente su [
p/2,
)si ha che
.è assolutamente integrabile in senso improprio su [p/2,) e quindi l'integrale improprio
è convergente
.Calcolare
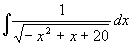
Svolgimento :
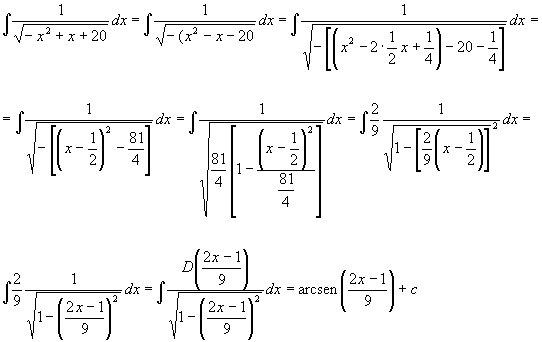
L’integrale dato può essere calcolato anche nel modo seguente:
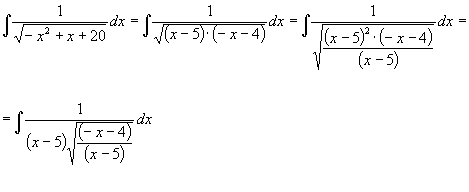
per sostituzione pongo
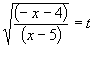
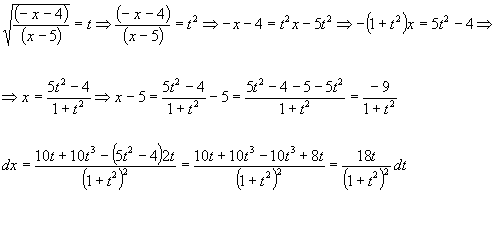
Quindi:
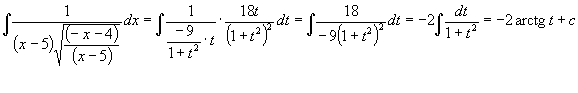
Sostituendo:
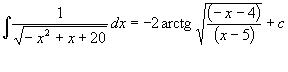
Studiare la convergenza della serie
Calcoliamo il raggio di convergenza della serie:
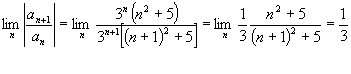
->il raggio di convergenza della serie è r=3 ,quindi la serie converge per 
.
Per x=3 otteniamo la serie
Essendo 
ed essendo convergente la serie
,
abbiamo che per il criterio del confronto la serie converge.
Per x=-3 otteniamo la serie
.
La successione 
è una successione a termini positivi, decrescente e infinitesima. Infatti
e
Quindi per il criterio di Leibniz, la serie converge.
Dunque la serie converge uniformemente nell’intervallo[-3,3].
Per 
la serie converge totalmente.
Infatti 
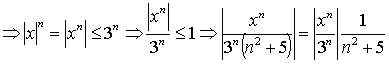
La serie è convergente e così la serie di potenze data converge totalmente in [-3,3].