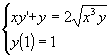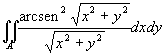Ritorna
a esercizi
COMPITO DI ANALISI MATEMATICA II
DEL 27/5/98.
Other exames
-
Studiare la convergenza della serie
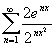
-
Calcolare il seguente integrale doppio
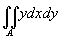
dove A=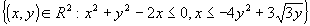
(P(0,0) e Q(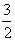 ,
,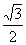 )
sono i punti di intersezione della circonferenza con la parabola)
)
sono i punti di intersezione della circonferenza con la parabola)
-
Calcolare l'area del domini regolare dalla curva di equazioni
parametriche x=
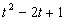 , y=t-1 con t
, y=t-1 con t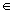
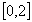
 e
dal segmento congiungente i suoi estremi.
e
dal segmento congiungente i suoi estremi.
-
Determinare il massimo e il minimo della funzione
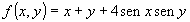
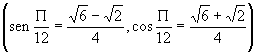
nel quadrato di vertici (0,0),(P
,0),(0,P ),(P ,P
)
-
 Determinare l'integrale
dell'equazione
Determinare l'integrale
dell'equazione 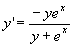 passante per il punto (1,2).
passante per il punto (1,2).
COMPITO DI ANALISI MATEMATICA 2
DEL 24/02/1999
Other exames
-
Studiare la convergenza puntuale ed uniforme della serie
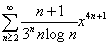
-
Studiare il problema di Cauchy
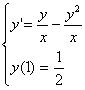
e determinare il prolungamento massimale della soluzione.
-
determinare inizialmente i punti di massimo e di minimo relativo
della funzione
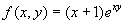 e
successivamente l’estremo superiore ed inferiore della funzione al variare
del punto (x,y) sulla retta di equazione 3x+4y=25.
e
successivamente l’estremo superiore ed inferiore della funzione al variare
del punto (x,y) sulla retta di equazione 3x+4y=25.
-
Sia B l’insieme delimitato da due circonferenze; una di centro
l’origine e raggio
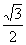 e l’altra
di centro
e l’altra
di centro 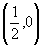 e raggio
e raggio 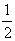 e
tratteggiato in figura. Calcolare l’area di B.
e
tratteggiato in figura. Calcolare l’area di B.
-
Calcolare l’area del dominio D la cui frontiera è
l’unione di due curve
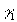 e
e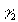 .
La prima è l’unione del segmento che congiunge i punti A=(2r,0)
e B=(0,2r) con r
.
La prima è l’unione del segmento che congiunge i punti A=(2r,0)
e B=(0,2r) con r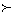 0 e dell’arco
di circonferenza di centro l’origine e raggio 2r congiungente i punti A
e B in senso orario, e la seconda
0 e dell’arco
di circonferenza di centro l’origine e raggio 2r congiungente i punti A
e B in senso orario, e la seconda 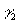 ha
equazioni parametriche
ha
equazioni parametriche
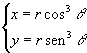
COMPITO DI ANALISI MATEMATICA II
DEL 26\05\1999
Other exames
-
Studiare la convergenza puntuale ed uniforme della serie
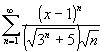

-
Studiare il problema di Cauchy
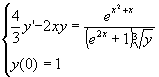
-
Determinare il volume del dominio normale T di R3
definito dalle limitazioni
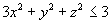
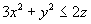
-
Dire se è esatta la seguente forma differenziale
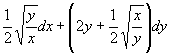
considerata nel suo insieme di definizione. Calcolare
l'integrale della forma lungo l'arco di parabola che va dall'origine al
punto (1,1).
-
Trovare l'insieme di definizione E della funzione
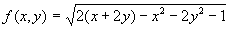 Trovare ,inoltre, se esistono, il massimo e il minimo assoluti di f in
E.
Trovare ,inoltre, se esistono, il massimo e il minimo assoluti di f in
E.
COMPITO DI ANALISI MATEMATICA II
DEL 16/06/1999
Other exames
-
Studiare la convergenza puntuale ed uniforme della serie

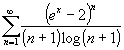
-
Studiare il problema di Cauchy
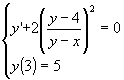
-
Calcolare
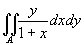
-
Studiare le proprietà di connessione dell’insieme
di definizione della forma differenziale
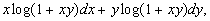
dire se è esatta e trovarne, eventualmente, la
primitiva. Calcolare l’integrale della forma lungo il segmento di primo
estremo (1,0) e secondo estremo (2,2).
-
Determinare i punti di massimo e di minimo relativo delle
funzioni y=y(x) definite implicitamente dall’equazione
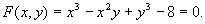


PROVA SCRITTA DI ANALISI MATEMATICA 2
DEL 13\07\99
Other exames
-
Determinare la convergenza puntuale ed uniforme
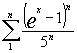
-
Calcolare
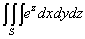
dove S è l’intersezione della palla unitaria con
il cono
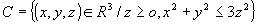
-
Determinare massimi e minimi relativi delle funzioni y=y(x)
definite implicitamente dalle equazioni F (x,y)= x4 + xy2
+
y4 = 0 tralasciando i punti singolari
-
Trovare l’area del dominio limitato dalle curve:
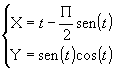
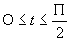
-
Risolvere il problema di Cauchy
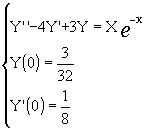
PROVA SCRITTA DI ANALISI MATEMATICA 2
DEL 29/09/99
Other exames
-
Determinare la convergenza puntuale ed uniforme
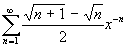
-
Calcolare
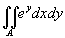
dove A =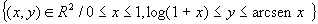
-
determinare massimi e minimi relativi della funzione y=y(x)
non negativa
definita implicitamente in 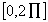 dall’equazione
dall’equazione
F(x,y)=-cosx+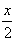 -y
-y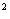 +1=0
+1=0
-
Trovare l’insieme di definizione della forma differenziale
e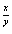 dx+(1-
dx+(1- )e
)e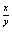 dy
dy
Calcolare l’integrale curvilineo della forma differenziale
lungo il segmento congiungente il punto (0,1) con il punto (2,3).
Dire se la forma è esatta nell’aperto 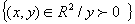 e
trovarne la primitiva .
e
trovarne la primitiva .
-
Risolvere il problema di Cauchy
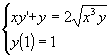
COMPITO DI ANALISI MATEMATICA II
27/10/1999
Other exames
-
Studiare la convergenza puntuale ed uniforme della serie
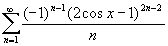
-
Studiare il problema di Cauchy
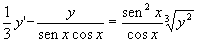
-
Calcolare

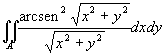
-
si calcoli il seguente integrale
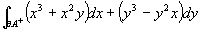 ,
,
dove A è la porzione del cerchio unitario contenuta
nel primo quadrante.
-
Dire se la forma differenziale
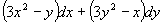 è chiusa ed esatta in
è chiusa ed esatta in 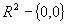 .Inoltre
verificare che è esatta nel semipiano x>0 e calcolarne in tale insieme
una primitiva. Determinare inizialmente i punti di massimo e di minimo
relativo e successivamente l'estremo superiore ed inferiore della funzione
.Inoltre
verificare che è esatta nel semipiano x>0 e calcolarne in tale insieme
una primitiva. Determinare inizialmente i punti di massimo e di minimo
relativo e successivamente l'estremo superiore ed inferiore della funzione 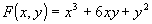 al variare del punto
al variare del punto 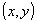 sulla
retta di equazione
sulla
retta di equazione 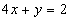 .
.
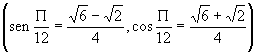
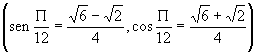
![]()
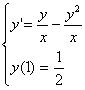
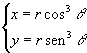
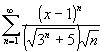
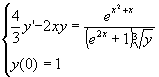
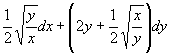
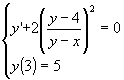
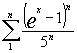
![]()
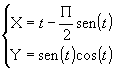
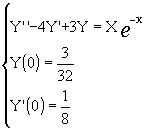
![]() e
trovarne la primitiva .
e
trovarne la primitiva .