PROVA SCRITTA DI ANALISI MATEMATICA 2

DEL 29-11-2000

 

1) Studiare la convergenza puntuale e totale della serie:

soluzione

 

  1. Calcolare l’integrale doppio:

    2. soluzione

    dove Q è la parte di corona circolare di centro l’origine e raggi 1 e 2 compresa tra le rette e con .

     

  2. Risolvere il problema di Cauchy:

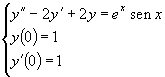    3. soluzione

     

  3. Stabilire mediante i teoremi di confronto se il seguente integrale:

    4. è o non è convergente e in caso affermativo calcolarne il valore. soluzione

     

  4. Dimostrare che la forma differenziale:

è esatta nel suo insieme di definizione. Determinare una primitiva e l’integrale della forma differenziale lungo l’arco della circonferenza di centro l’origine e raggio 2, di estremi e orientato in senso antiorario. soluzione

ritorna all’indice